벨만-포드 알고리즘 (Bellman-Ford Algorithm)
벨먼-포드 알고리즘은 가중 유향 그래프에서 최단 경로 문제를 푸는 알고리즘이다. 이때 변의 가중치는 음수일 수도 있다.
데이크스트라 알고리즘은 벨먼-포드 알고리즘과 동일한 작업을 수행하고 실행속도도 더 빠르다.- 위키 백과
벨만 포드 알고리즘은 그래프 내에서 최단 경로를 찾는 알고리즘입니다.
그래프 내에서 최단 거리를 찾는 알고리즘에는 '다익스트라 알고리즘'이 존재하는데, 벨만 포드 알고리즘을 사용하는 이유는 무엇일까요?
바로, 간선의 가중치가 음수인 경우에 대비할 수 있기 때문입니다.
가중치가 음수인 간선
가중치가 음수인 간선이 존재한다고 해서 다익스트라 알고리즘을 사용할 수 없는 것은 아닙니다.
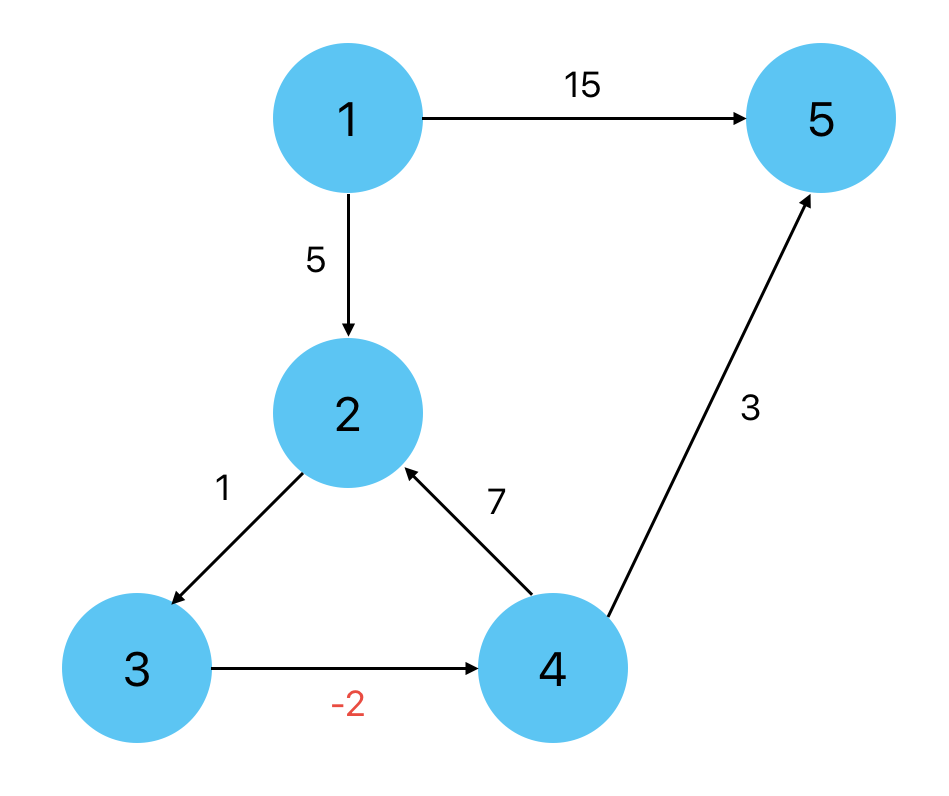
만약 다음과 같은 그래프가 있다면, 최단 경로는 1-2-3-4-5 일 것입니다. 음수인 간선이 있어도 정상적으로 최단 경로를 구할 수 있습니다.
음의 사이클
하지만, 다음과 같은 경우에는 어떨까요?
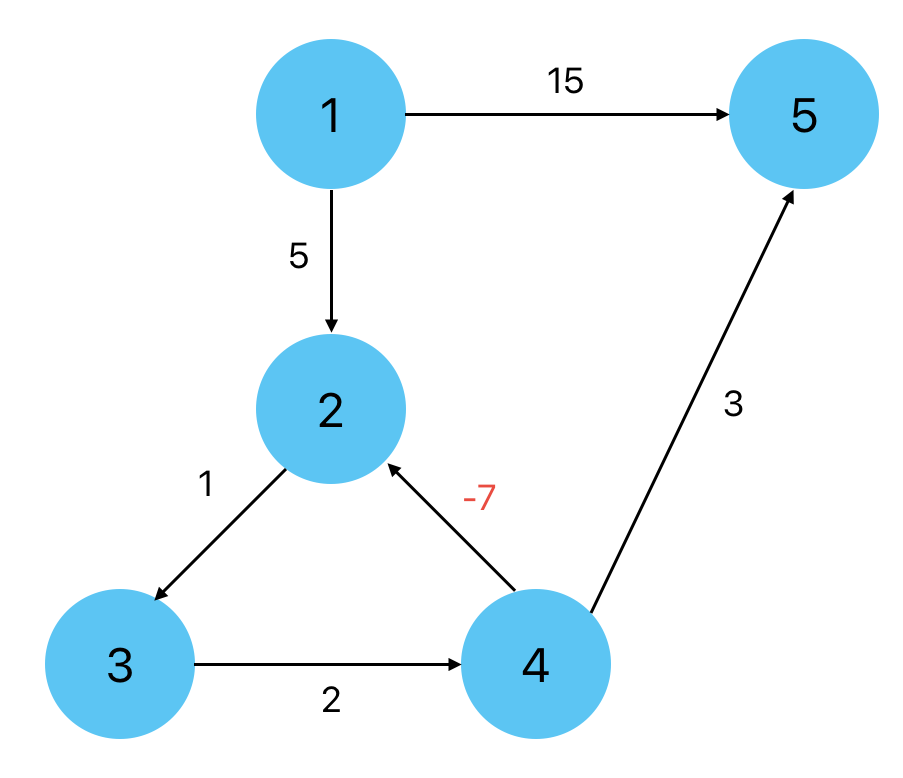
그림의 2, 3, 4번 노드는 사이클을 이루고 있고, 2번 노드에서 시작하여 사이클을 한 바퀴 돌고나서 다시 2번 노드로 오게 되면 거리는 -4가 됩니다.
그렇다면 계속해서 사이클을 돈다면 이동 거리는 음의 무한대가 되는 현상이 발생합니다.
다익스트라 알고리즘을 사용한다면 저 음의 사이클을 계속해서 이동하게 되어 사용이 불가능합니다.
음의 사이클 감지
위와 같은 문제를 해결하기 위해 벨만-포드 알고리즘을 사용합니다.
벨만 포드 알고리즘은 어떻게 해서 위의 문제를 해결할 수 있을까요?
문제가 되는 이유는 음의 사이클이 존재하고 그것을 알지 못하기 때문에 계속해서 이동하게 되기 때문이었습니다.
그래서 벨만 포드 알고리즘에서는 음의 사이클을 감지 하여, 만약 음의 사이클이 감지되었다면 최단 거리를 찾을 수 없다는 반환값을 return하게 됩니다.
감지 과정
음의 사이클을 감지하는 과정은 다음과 같습니다.
모든 노드까지의 거리를 INF로 초기화하고, 출발 노드의 거리는 0으로 초기화합니다.
모든 간선을 탐색하며 최단 거리를 갱신합니다.
2번의 과정을 (노드의 개수-1)번 반복합니다.
3번까지의 과정에서, 이미 최단 거리 갱신이 완료 되었어야 합니다. 그렇기 때문에 만약 2번의 과정을 한 번 더 수행했을 때 최단 거리가 갱신된다면 음의 사이클이 존재한다고 판단할 수 있습니다. 음의 사이클이 존재한다면 return False등을 하여 최단 거리를 구하는 것이 불가능 함을 알립니다.
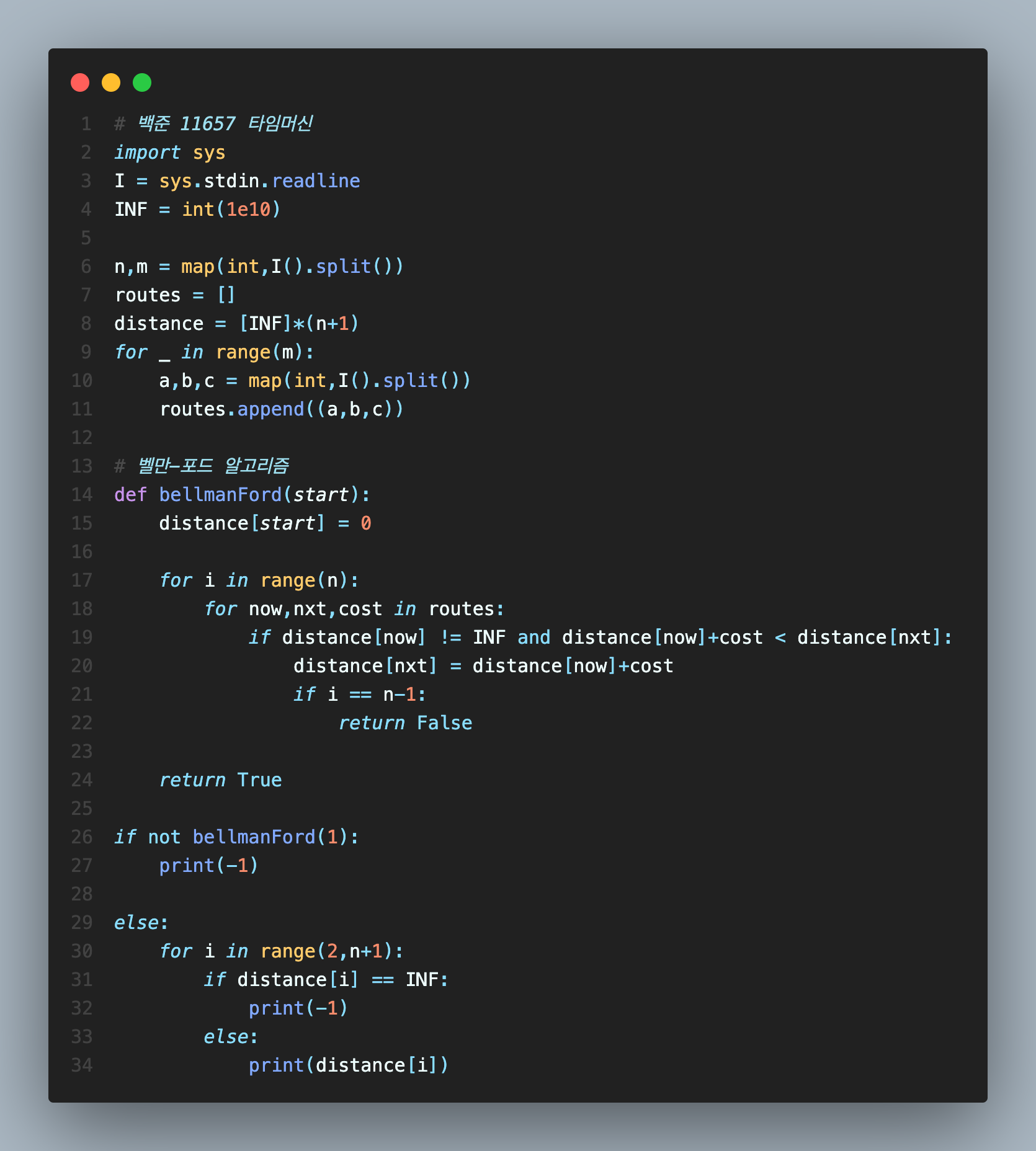
코드 (파이썬)

0개의 댓글