크루스칼 알고리즘 (Kruskal Algorithm)
컴퓨터 과학에서 크러스컬 알고리즘(영어: Kruskal’s algorithm)은 최소 비용 신장 부분 트리를 찾는 알고리즘이다.
- 위키백과
최소 신장 트리
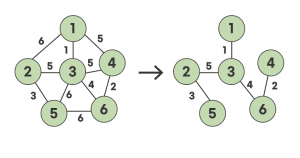
(이미지 출처: 포스테키안 - 2021 여름호 / 지식더하기 ②)
최소 신장 트리란, 그래프 내부의 모든 노드를 연결 시키면서 그 비용이 최소가 되는 트리를 말합니다.
모든 노드를 연결한다는 점과, 비용이 최소가 되어야 한다는 점 때문에 간선의 개수는 (노드의 개수 - 1)개가 되고, 그렇기에 트리라고 할 수 있습니다.
최소 신장 트리 만들기
최소 신장 트리를 만들기 위해서는 그리디 알고리즘을 사용합니다. 그 과정은 다음과 같습니다.

모든 간선을 비용이 적은 순서대로 정렬합니다 (오름차순)
1번의 결과를 0번 인덱스부터 loop를 돌며, 간선의 양 끝 노드가 현재 연결된 상태인지 아닌지를 체크합니다.
만약 두 노드가 연결되어있지 않다면 해당 간선을 사용하여 연결하고, 이미 연결되어 있다면 무시합니다.
모든 노드가 연결될 때 까지 2, 3번을 반복합니다.
과정은 매우 간단합니다.
최소 비용으로 연결해야 하기 때문에, 최소인 간선들을 먼저 사용하여 모든 노드가 연결될 때 까지만 반복하면 되는 것입니다.
하지만 두 노드가 연결 되어 있는 상태인지, 모든 노드가 연결된 상태인지 알 수 있는 방법에 대해서는 아직 알지 못하기 때문에 이에 대해 알아보겠습니다.
서로소 집합
각각의 노드는 연결 상태에 따라 여러 집합으로 나눌 수 있습니다.
만약 1~5번 노드가 존재할 때, 1,2번 노드만 서로 연결되어 있고 4,5번 노드만 서로 연결되어 있다면 집합은 (1,2), (3), (4,5) 와 같이 나눌 수 있을 것입니다.
이 방법을 크루스칼 알고리즘에 사용한다면, 두 노드가 같은 집합에 있다면 연결된 상태이고, 두 노드가 다른 집합에 있다면 연결되지 않은 상태라고 판단할 수 있을 것입니다.
서로소 집합 판단
두 노드가 같은 집합에 있는 지 판단하는 기준은 바로 공통된 부모를 가지고 있는가? 입니다.
그리고 집합 내부의 부모는 보통 집합 내부에서 가장 작은 번호의 노드입니다.
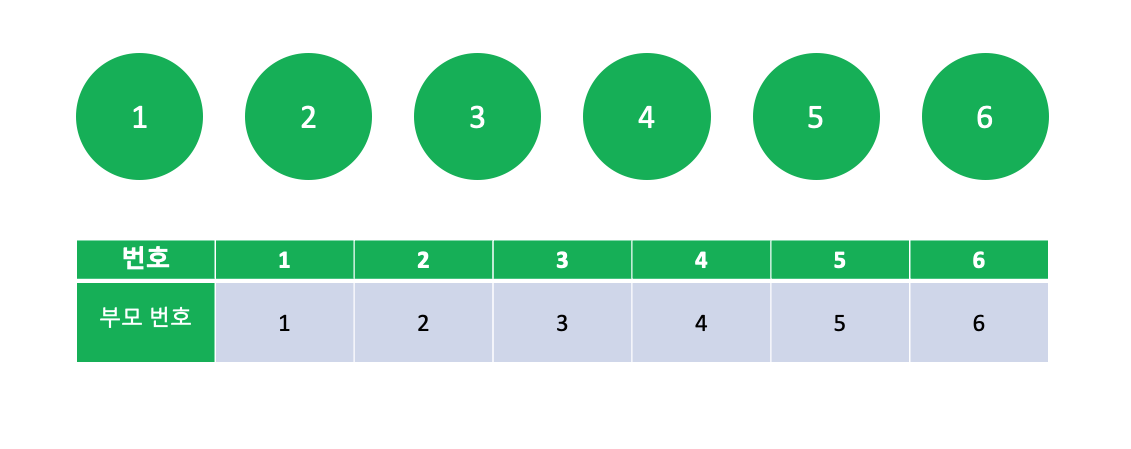
다음과 같이 1~6번 노드가 있고, 아직 누구도 연결되지 않은 상태라고 해봅시다.
이 때, 부모는 자기 자신이라고 할 수 있습니다. 누구도 연결되지 않았기 때문에 각각의 노드가 분리된 집합에 있는 것이고, 그렇기에 그 집합 내에서 가장 번호가 작은 노드도 자신이 되기 때문입니다.
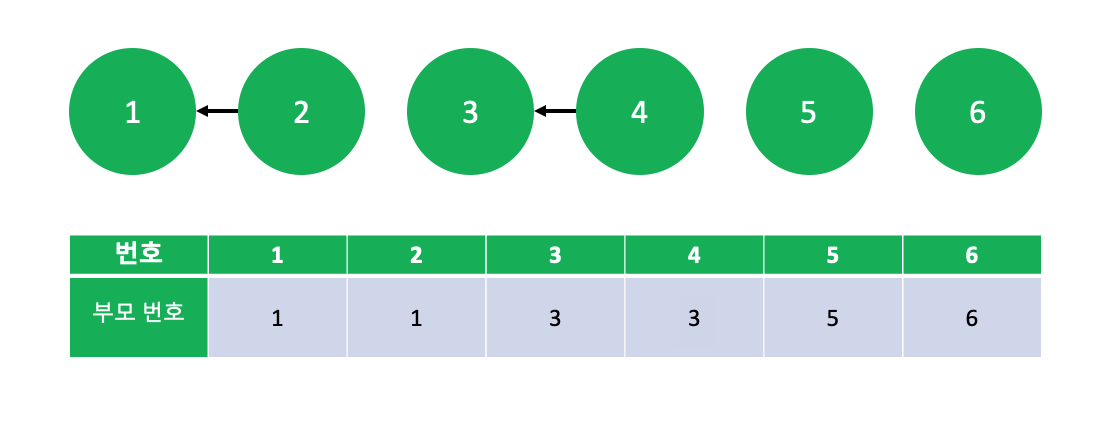
이 그림처럼 1-2번 노드가 연결 되고, 3-4번 노드가 연결 되었다고 한다면, 1번과 2번 중 번호가 작은 노드는 1번이므로 2번의 부모가 1번이 되고, 3번과 4번 역시 마찬가지입니다.
그리고 (1,2)와 (3,4)는 부모가 같기 때문에 같은 집합에 속한 노드라고 생각할 수 있습니다.
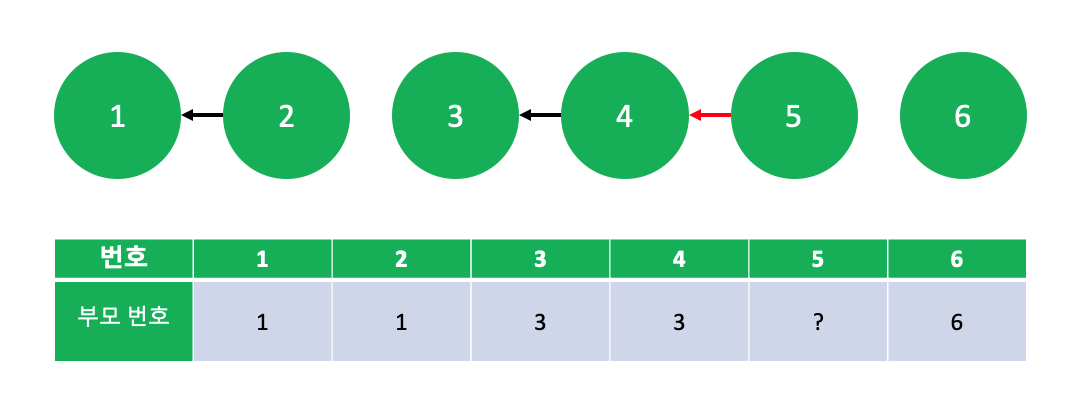
5번노드가 4번노드와 연결 되었다고 생각해보면, 4번과 5번 중 작은 번호는 4번이기 때문에 4번노드가 5번 노드의 부모가 되어야 할 것입니다.
여기서, 4번 노드의 부모는 이미 3번 노드로 갱신되었기 때문에, 5번 노드도 3번 노드를 부모로 가지게 됩니다.

위의 경우처럼, 부모가 자기 자신이 아닌 다른 노드로 변경된 경우 이를 찾기 위해 재귀 함수를 사용합니다.
현재 탐색 중인 이 노드의 부모는 자기 자신이라면 (즉, 집합에 속한 노드들 중 가장 작은 번호의 노드라면) 그대로 parent[x]를 return 한다.
그렇지 않다면, 이 노드의 부모의 부모를 찾기 위해 재귀 함수에 부모 노드를 넣는다.
1번이 될 때까지 2번을 반복한다.
서로소 집합 연결

두 서로소 집합을 연결할 때, 앞서 보여드린 findParent함수와 위의 unionParent 함수를 사용합니다.
연결 과정은 다음과 같습니다.
연결하려는 두 노드의 부모를 갱신합니다. (갱신 되지 않은 상태일 때의 오류를 피하기 위함)
두 노드의 부모가 다르다면 (즉, 연결되지 않은 서로소 집합이라면) union과정을 수행합니다.
Union과정은, 두 노드 중 '부모 노드의 번호가 큰 노드'의 부모를 작은 노드의 부모 노드로 변경하는 것입니다. (예를 들어, a와 b라는 노드가 있고 a의 부모는 1, b의 부모는 2라고 했을 때 2 > 1이기 때문에 b의 부모를 a의 부모인 1로 갱신하는 것입니다.)
크루스칼 알고리즘 예시 코드
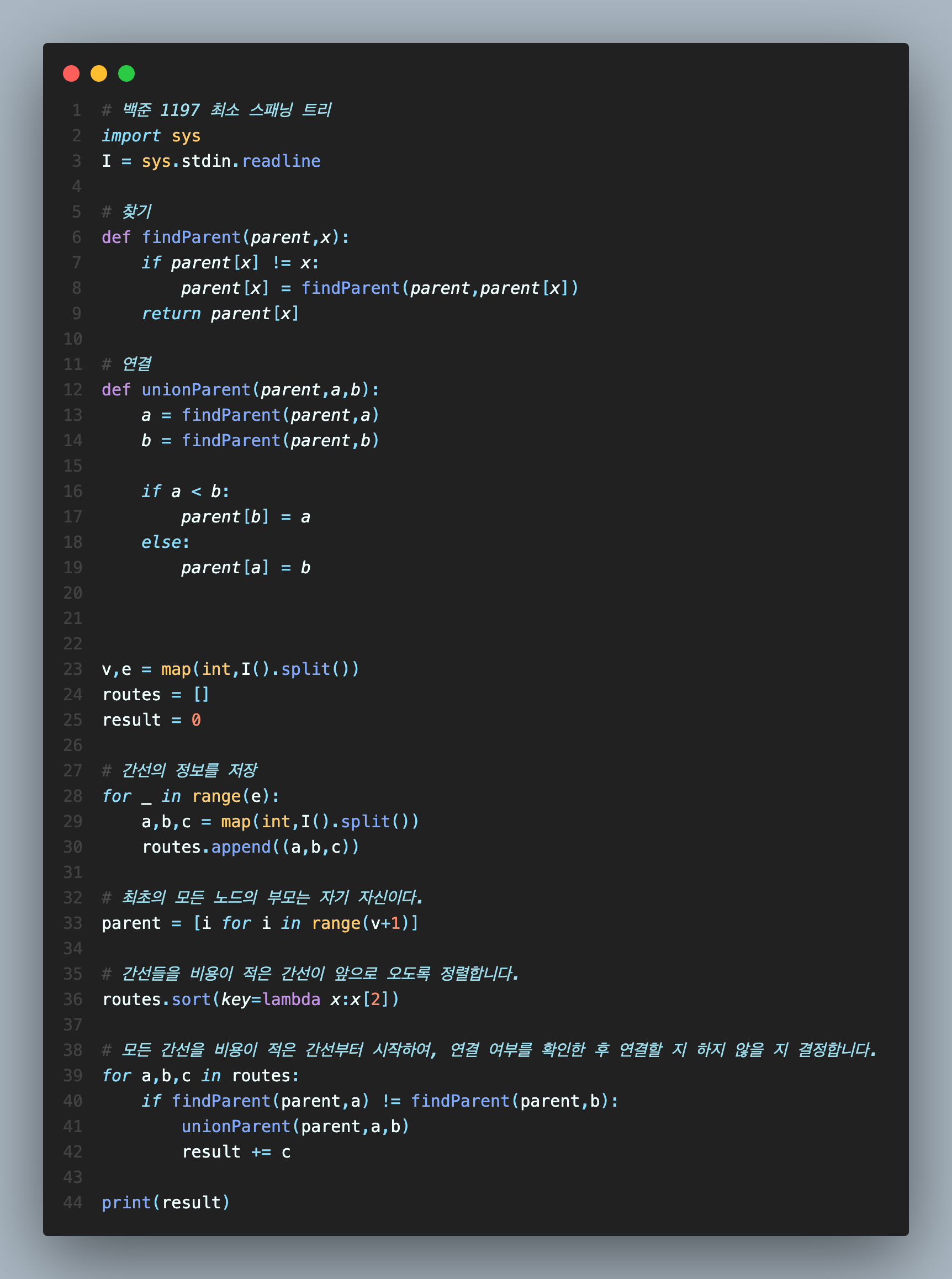
앞서 설명한 서로소 집합을 사용하여 크루스칼 알고리즘을 수행하는 예시 입니다.

0개의 댓글