[프로그래머스] 연속 펄스 부분 수열의 합 LV.3

[프로그래머스] 연속 펄스 부분 수열의 합 LV.3

문제

어떤 수열의 연속 부분 수열에 같은 길이의 펄스 수열을 각 원소끼리 곱하여 연속 펄스 부분 수열을 만들려 합니다. 펄스 수열이란 [1, -1, 1, -1 …] 또는 [-1, 1, -1, 1 …] 과 같이 1 또는 -1로 시작하면서 1과 -1이 번갈아 나오는 수열입니다.예를 들어 수열 [2, 3, -6, 1, 3, -1, 2, 4]의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하면 연속 펄스 부분수열은 [3, 6, 1]이 됩니다. 또 다른 예시로 연속 부분 수열 [3, -1, 2, 4]에 펄스 수열 [-1, 1, -1, 1]을 곱하면 연속 펄스 부분수열은 [-3, -1, -2, 4]이 됩니다.정수 수열 sequence가 매개변수로 주어질 때, 연속 펄스 부분 수열의 합 중 가장 큰 것을 return 하도록 solution 함수를 완성해주세요.

발상

1. 연속 펄스 부분 수열의 합을 구하는 것이기 때문에 구간 합을 사용한다.

2. 연속 펄스 부분 수열은 [-1,1,-1,1,...] 또는 [1,-1,1,-1,...]의 두 가지 패턴 만이 존재한다.

3. 예시 sequence에서 두 패턴의 구간 합을 구해보면 부호만 반대인 완전히 같은 결과가 나온다.

4. 두 패턴 중 하나의 구간 합 만을 구하고, 최소 값과 최대 값의 차이의 절댓값을 구하면 답이 된다.

이유

우선, 구간 합이 최대가 되려면 구간합이 최대가 되는 지점에서 최소가 되는 지점을 빼주면 된다

ex) 구간 합이 [0,-2,1,7,8,5,4,2,6]인 경우, 최대 구간합은 8-(-2) = 10이다.

하지만 펄스 수열이 반대인 경우의 구간 합을 구한 경우, 구간 합은 [0,2,-1,-7,-8,-5,-4,-2,-6]이 된다.

이 경우에 펄스 수열을 반대로 곱해주었다면 답은 위의 예시와 같이 10이 되지만 이 경우에는 -10이 된다.

그렇기 때문에 구간 합의 절댓값이 최대가 되는 경우가 답인 것이다. (반대 펄스 수열을 곱해주면 되기 때문)

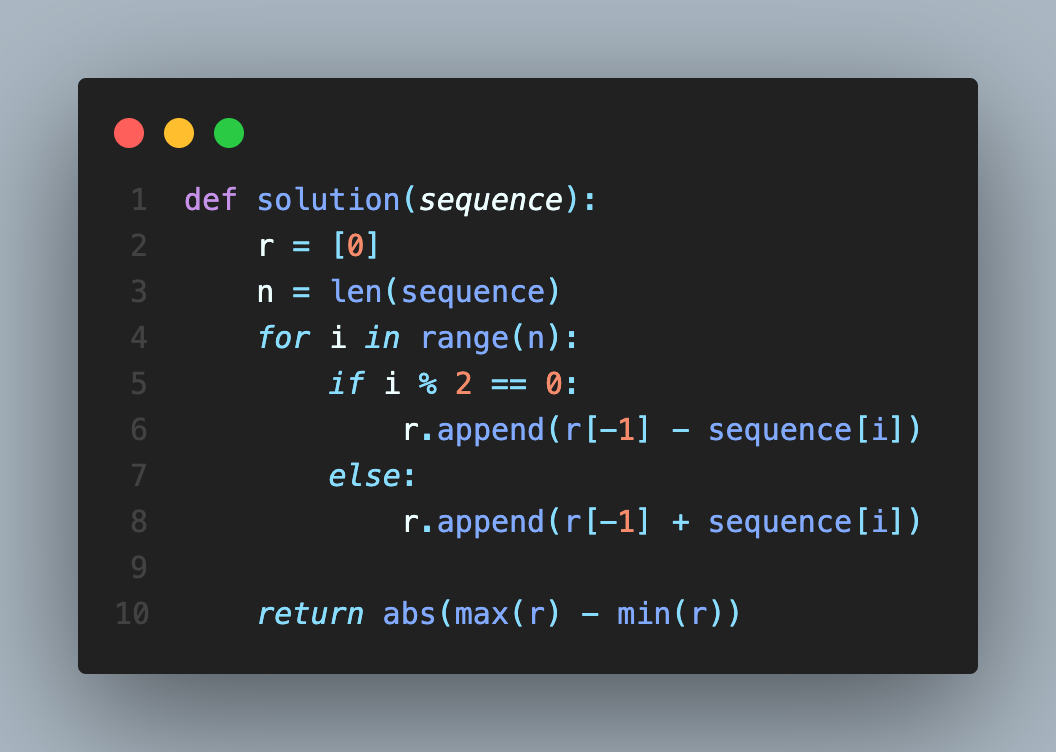
코드